Answer: It is a normal density with center μ = 1 and spread σ = 1.
Answer: First compute the z-score z = (120 - 100) / 15 = 20 / 15 = 1.33.
Then area[1.33, ∞) = 1 - area(-∞, 1.33] = 1 - 0.9082 = 0.0918 = 9%. Here is the R calculation:
(1 - pnorm(120, mean=100, sd=15) [1] 0.09121122
Answer: z = (x - mu) / sigma = (175 - 100) / 15 = 5. to see that the proportion of scores greater than 5 is 2.867 × 10-7. Multiply this proportion by 1 billion = 109 to see how many persons out of one billion have an IQ score greater than 175:
2.867 × 10-7 * 109 = 286.7 ≈ 287. The R calculation:
(1 - pnorm(175, mean=100, sd=15)) * 1.0e9 [1] 286.6516
Answer: look up 0.9 in the second normal table and read the z-value in the margins of the table 1.28. Then convert this z-value to an IQ score: z * sd + mean = 1.28 * 15 + 100 = 119.2. The R calculation:
qnorm(0.9, mean=100, sd=15) [1] 119.2233
Unbiased means the data have the same mean in any thin rectangle all the way across the plot.
Biased means the data do not have the same mean in every thin rectangle.
Homoscedastic means that the data have the same standard deviation in every thin rectangle.
Heteroscedastic means that the data do not have the same SD in every thin rectangle.
y1 <- y y2 <- y * (x / 100) y3 <- y + (x - 100) * 0.05 y4 <- y * x / 100 + (x - 100) * 0.025Classify each plot as unbiased or biased; homoscedastic or heteroscedastic.
Answer: set up the vector of observation numbers and normal random values:
x <- 1:100 y <- rnorm(100)Then create four plots:
Plot 1:
> y1 <- y > plot(x, y1, xlab="Observation Number", + ylab="Dataset Values", + main="Unbiased and Homoscedastic")

Plot 2:
> y2 <- y * (x / 100) > plot(x, y2, xlab="Observation Number", + ylab="Dataset Values", + main="Unbiased and Heteroscedastic")
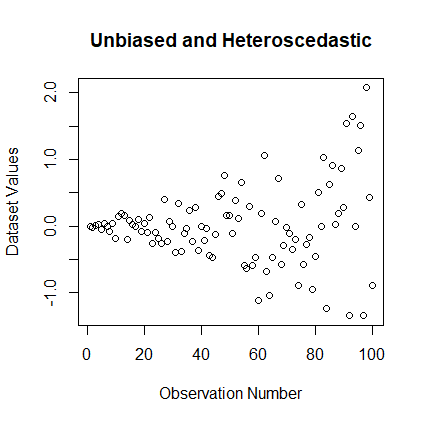
Plot 3:
y3 <- y + (x - 100) * 0.025 plot(x, y3, xlab="Observation Number", + ylab="Dataset Values", + main="Biased and Homoscedastic")

Plot 4:
> y4 <- y * x / 100 + (x - 100) * 0.025 > plot(x, y4, xlab="Observation Number", + ylab="Dataset Values", + main="Biased and Heteroscedastic")


