Jan 14, 2026

IT 223 -- Jan 14, 2026

Review Problems

Modify the R statements that we used to create the vector w of weight measurements for NIST-10 dataset, to show what the R dataframe for Weight looks like. Answer: execute these statements one at a time

# Set the working directory to "C:/workspace".
setwd("C:/workspace")

# Check the resulting working directory.
# It should be "C:/workspace".
getwd( )

# Display all files in the working directory
dir( )

# Create an R dataframe from the CSV file
# nist-10.txt. CSV means comma separated value.
weightDf <- read.csv("nist-10.txt")

# Print the resulting data frame.
print(weightDf)

# Extract the Weight column from the dataframe:
w <- weightDf$Weight

# Print the extracted weight vector w.
print(w)

Use these R statements to create a graph of a normal curve:
```
x <- seq(-4, 4, 0.05)
y <- dnorm(x)
plot(x, y, type="l")
```
Answer: Here is the resulting R graph of the normal density:
Show that when the histogram bins are all the same width, the height of the bars is the count or frequency in each bin. However, when the widths of the bins are not equal, the vertical axis represents a density, with the vertical axis being Percent per Horizontal Unit. In the second case, the area of the bar represents the percentage of observations in that bin.
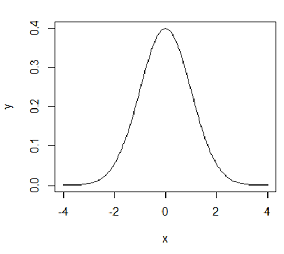
Answer: Create one histogram with equal bin widths: [0, 1], (1, 2], and another histogram with unequal bin widths: [0, 1], (1, 4].
```
x <- c(0.5, 0.5, 0.5, 1.5, 1.5)
b1 <- c(0, 1, 2)
b2 <- c(0, 1, 4)
hist(x, breaks=b1, main="Equal Width Bins")
hist(x, breaks=b2, main="Unequal Width Bins")
```
The resulting histograms:

For the Equal Width Bins histogram, the vertical axis label is Frequency and the vertical units are the counts in each bin; for the Unequal Bin Widths histogram, the vertical label is Density and the vertical units are fraction of observations per horizontal unit.
What is a critical point for a curve?
Ans: a critical point of a curve is where the slope of the curve is horizontal For a normal curve, the x-value of the critical point is the maximum value of the curve. The normal curve is symmetric around the center.
What is an inflection point for a curve?
Answer: an inflection point of a curve is where the curve changes from concave down to concave up, or vice versa.
What is the sample mean?
Answer: the sample mean is another name for the sample average. If x₁, x₂, ... , x_n is the dataset, the sample mean is the sum of the observations divided by the number of the observations:
X = (x₁ + x₂ + ... + x_n) / n

Descriptive Statistics

If a histogram (drawn without vertical bar lines) is bell-shaped or normal, it can be described by its center μ and spread σ:
For a bell-shaped histogram, if the sample size n is large, the statistics x (sample average) and SD+ (sample standard deviation) are good estimates of μ and σ.
x and SD+ form a parsimonious description of a bell-shaped histogram.
The sample average is also called the sample mean.
Estimates of the Center of a Dataset: Mean Median Trimmed Mean
Estimators of the Spread of a Dataset: SD SD⁺ MAD

Practice Problems

What happens to x and Q2 for a dataset
1. if every observation is increased by 7?
  Ans: Both x and Q2 are increased by 7.
  x_new = (x₁ + 7 + ... + x_n + 7) / n
  = (x₁ + ... + x_n) / n + (7 + ... + 7) / n
  = x + n 7 / n = x + 7
2. if every observation is multiplied by 3?
  Answer: Both x and Q2 are multiplied by 3.
  x_new = (3x₁ + ... + 3x_n) / n
  = 3(x₁ + ... + x_n) / n = 3 x
3. if the largest observation is increased by 1000?
  Ans: The mean is increased by 1000 / n, the median is unchanged if n ≥ 3.
  (1/n)(x₁ + ... + (x_n + 1000)) = x + 1000 / n
What happens to SD for a dataset if
1. if every observation is increased by 7?
  Ans: the SD is unchanged because the spread is unchanged.
2. if every observation is multiplied by 3?
  Ans: the SD is multiplied by 3 because the spread is multiplied by 3.
Compute the 20%-trimmed mean of this dataset:
1 7 4 6 94 5 5 7 3 6
Answer: Trimming 10% of the variables off of the bottom and 10% off of the top, means omitting 1 and 94. The average of the remaining variables is 5.375.
Perform this calculation using R. Answer: if x is the complete dataset, use
```
mean(x, trim=0.05)
```
where trim=0.05 means trim 0.05 of the observations from the left and 0.05 of the observations from the right.
Without doing any calculations, compute the SD of this dataset:
4 4 4 4 4
Without doing any calculations, compute the SD of this dataset:
0 0 0 0 10 10 10 10
Use R to compute SD+ of the hypothetical exam scores.
Compute the MAD of this dataset:
20 10 15 15

Computing the Mean of a Histogram

Practice Problem: Compute the sample means of the histograms in More Review Exercises, Exercise 1a, 1b, and 1c of the Jan 7 Notes. Use a weighted average of the midpoints of each rectangle weighted by the proportion of observations represented by that rectangle.
Answer: Compute the weighted average (x₁ w₁ + ... + x_n w_n) / (w₁ + ... + w_n) , where x₁ is the midpoint of the ith bin and w₁ is the number or proportion of observations in the ith bin.

Answer for (a):
Calculation using numbers of observations in the 
bins for weights:  
0.5 * 1 + 1.5 * 3 + 2.5 * 5 + 3.5 * 1   21
------------------------------------- = --- = 2.1
            1 + 3 + 5 + 1               10

Calculation using percentages of observations in the
bins for weights:  
0.5 * 10 + 1.5 * 30 + 2.5 * 50 + 3.5 * 10   210
----------------------------------------- = --- = 2.1
            10 + 30 + 50 + 10               100

Calculation using proportions of observations in the 
bins for weights:  
0.5 * 0.1 + 1.5 * 0.3 + 2.5 * 0.5 + 3.5 * 0.1   2.1
--------------------------------------------- = --- = 2.1
            0.1 + 0.3 + 0.5 + 0.1                1

Ans for (b):
Use percentages for weights
0.5 * 30 + 1.5 * 50 + 3.0 * 20    150
------------------------------ =  --- = 1.5
         30 + 50 + 20             100

Ans for (c):  
Use percentages for weights:
 0.5 * 20 + 1.5 * 40 + 2.25 * 30 + 2.75 * 10   165
 ------------------------------------------- = --- = 1.65.
               20 + 40 + 30 + 10               100

The Ideal Measurement Model

No measurement is perfect.
Every measurement involves some random error and systematic bias.
The ideal measurement model assumes that a set of measurements has no systematic bias, and that the random errors are independent with the same standard deviation everywhere (homoscedastic).
More details on the Ideal Measurement Model.

Analyze the NBS-10 Dataset

Use R to obtain the following for the NIST-10 and PaperThickness datasets:

x and SD+
Histograms with three different bin widths
Outliers using the boxplot

Answer: the R statements for the PaperThickness dataset:

setwd("workspace")
thicknessDf <- read.csv("paper-thickness.txt")
t <- thicknessDf$Thickness
mean(t)
sd(t)
range(t)
# Default histogram
hist(t)
# Histogram with less breaks than default.
hist(t, breaks=c(0.09, 0.10, 0.11, 0.12))
# Histogram with more breaks than default.
hist(t, breaks=seq(0.09, 0.12, 0.001))
boxplot(t)

Warning: do not automatically delete the outliers from the dataset. They may be the most important observations in the dataset.
Here is a story (that might be an urban legend) about deleting outliers. Climatologists were studying the ozone levels in the upper atmosphere at the South Pole. In the 1960s, it was common for engineers to routinely delete outliers from the dataset, suspecting that they were bad observations. One of the data analysts therefore was deleting outliers from the Ozone observations dataset. Because of this, the hole in the ozone layer at the South pole was discovered several years later than it should have been.

Project 2

Go over Project 2a.